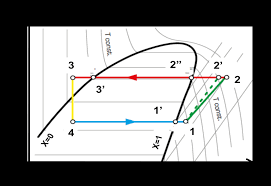
Ce module vise à appliquer les connaissances de thermodynamique acquises dans les modules précédents aux systèmes ouverts et fermés. L’accent est mis sur le fonctionnement et l’analyse des échangeurs, compresseurs, machines thermiques et machines frigorifiques, à travers l’étude de leurs cycles thermodynamiques respectifs. Il est destiné avant tout aux étudiants en science de la matière (3ème année LMD physique énergétique). Il s'adresse aussi aux étudiants des autres paliers d’enseignement supérieur qui voudraient élargir leurs connaissances en thermodynamique.
- Enseignant: Fatma Zohra FOUDDAD
Dans la théorie des fluides parfaits incompressibles, la répartition des vitesses, des pressions et
la forme des lignes de courant sont, en général, déterminées par la géométrie des parois limitant
l’écoulement, et ne dépendent pas de la nature du fluide envisagé.
L’étude des fluides réels (visqueux), a montré que les solutions proposées par cette théorie sont
conformes aux données expérimentales, si on considère les zones éloignées des parois. Mais dans le
voisinage immédiat de celles-ci, la théorie des fluides parfaits n’est plus valable. Ceci est dû au fait que
les conditions aux limites sont différentes dans les deux types des fluides.
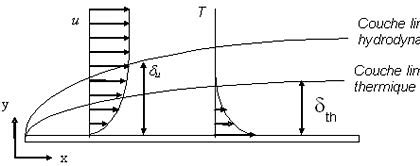
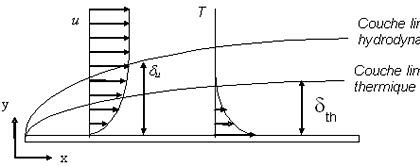
Dans le cas d’un fluide parfait, il n’y a pas de condition aux limites particulière pour la vitesse tangentielle d’une particule fluide sur une paroi solide. Elle peut, en particulier, être différente de 0 (la composante normale sera toujours nulle) à cause du glissement des particules sur les parois. Par contre pour un fluide visqueux il faudra écrire la nullité de la composante tangentielle à la surface de l’obstacle, cette dernière passe progressivement d’une valeur nulle (sur la paroi) à une valeur maximale dite vitesse de l’écoulement libre, prédite de manière acceptable par le modèle du fluide parfait.
Il existe donc, dans le voisinage des parois solides, une région ou l'écoulement change de caractère, dite couche limite. C’est cette région que nous nous proposons d’étudier dans ce chapitre.
- Enseignant: fares redouane